



Next: Indices
Up: Elucidation
Previous: Elucidation
Contents
How dimensions are specified
We consider the dimensions of a data object to be those quantities which are
used to select and categorize the data values. To understand the
nature of these dimensions, it may help to identify them with
the indices of a multi-dimensional array.
(This paradigm has its limits, though: data which cannot be described
in terms of a regular array can nevertheless be described in terms of
these dimensions.)
We have proposed four levels of these dimensions:
- Level 0
- dimensions describe the components of the data
(these dimensions are unrelated to the position of a datum in a coordinate
space). Simple scalar data such as temperature would have a
single Level 0 dimension containing a single
grid point (i.e, A Level 0 of order 1 with a rank of 1). A two-component
horizontal wind vector would also have a single Level 0 dimension, but
with two grid points (order of 1, rank of 2). A wind stress tensor (a
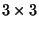 matrix) would have
two Level 0 dimensions, each of which would have three grid points (order
of 2, ranks of 3 and 3). In terms of array indices, Level 0 dimensions
select components at a fixed position. That is, a wind
stress tensor is
considered to be a datum, and
two Level 0 indices are
needed to select a single component of the tensor.
Likewise, a wind vector as a whole is a single item, but a Level 0 index
would select which component of the wind (North-South or East-West) is desired.
For temperature, there is only one component to select; this would
correspond to a single array index
which can take only a single value. (Because a
matrix) would have
two Level 0 dimensions, each of which would have three grid points (order
of 2, ranks of 3 and 3). In terms of array indices, Level 0 dimensions
select components at a fixed position. That is, a wind
stress tensor is
considered to be a datum, and
two Level 0 indices are
needed to select a single component of the tensor.
Likewise, a wind vector as a whole is a single item, but a Level 0 index
would select which component of the wind (North-South or East-West) is desired.
For temperature, there is only one component to select; this would
correspond to a single array index
which can take only a single value. (Because a 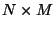 array is
indistinguishable from a
array is
indistinguishable from a
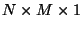 array, such an
index is superfluous and can be omitted.)
array, such an
index is superfluous and can be omitted.)
- Level 1
- dimensions are those that occur within a single data record.
- Level 2
- dimensions are those that occur across data records.
The Level 1 dimensions, together with the Level 2 dimensions,
locate a datum in a coordinate space. The difference between the two
levels is that Level 1 dimensions vary within a data record in the dataset,
while Level 2 dimensions vary between data records.
If each data record were read into a separate array variable, then every array
would have to have an index for each Level 0 and Level 1 dimension.
Suppose, for example,
that a set of temperatures is written out in a series of
two-dimensional longitude-latitude grids, one for each day. The resulting
dataset would have two Level 1 dimensions--longitude and latitude--plus
one Level 2 dimension: time.
This distinction between the two levels may seem artificial, but it
has two advantages: first, it enables a program to read the data
either as a single large array variable (whose indices would correspond to
each of the Level 0, Level 1, and Level 2 dimensions), or as a series
of separate variables (whose array indices correspond to each of the
Level 0 and Level 1 dimensions, with the number of arrays calculated from
the Level 2 dimensions). Second, if the data are read in as separate
arrays, then those arrays may be of different sizes. That is, the Level 1
dimensions may have different structures over different ranges of Level 2
dimensions. For example,
the first five days of the longitude-latitude wind fields might consist
of five
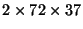 arrays, while the next ten days
might be a series of ten
arrays, while the next ten days
might be a series of ten
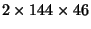 arrays.
arrays.
- Level 3
- dimensions specify how the data in the dataset
have been averaged, integrated, or summed over which subsets of
Level 0, Level 1, and Level 2 dimensions. These are
``virtual dimensions'', in that they do not correspond to any indices
in a data
array, but otherwise their structure is very similar to that of the other,
``real'' dimensions. A set of monthly averaged data, for example,
would have a Level 3 dimension corresponding to time and detailing
the days of the month over which the average was taken, as well as
what averaging method was used.
(Note that instantaneous or point data,
consisting of observations or calculations
that are considered to occur at fixed points in coordinate space,
have no averages and hence have no Level 3 dimensions.)
Dimensions may have multiple, parallel definitions. For example, pressure
levels at which data are recorded can also be specified as altitudes
above sea level. Which description is best? This is a decision best
left to the dataset
originator. The originator must define one quantity as the
authoritative descriptor for a given dimension;
any other descriptors for that same dimension will be duplicate,
additional descriptors for the dimension. A user of the data will use the
authoritative descriptor to obtain the definitive word on
the grid point values of that dimension;
users may use the additional information if they desire it, but that
information is not required for understanding the quantity that dimension
represents.




Next: Indices
Up: Elucidation
Previous: Elucidation
Contents
Eric Nash
2003-09-25
![]() arrays, while the next ten days
might be a series of ten
arrays, while the next ten days
might be a series of ten
![]() arrays.
arrays.